what is the prime factorization of 525 using exponents
Prime Factorization Computer
Please render an integer to find out its prime factors as swell as a factor tree.
What is a prime phone number?
Prime numbers are natural numbers (confident whole numbers that sometimes include 0 in certain definitions) that are greater than 1, that cannot be saddle-shaped by multiplying 2 smaller numbers game. An example of a prime number is 7, since information technology can single be formed by multiplying the numbers 1 and 7. Other examples include 2, 3, 5, 11, etc.
Numbers that can exist perfected with two other natural numbers, that are greater than 1, are called composite numbers. Examples of this admit numbers like, 4, 6, 9, etc.
Prime numbers racket are widely used in number theory referable the fundamental theorem of arithmetic. This theorem states that natural numbers greater than 1 are either prime, or can be factored as a production of prime Numbers. As an example, the number 60 buttocks be factored into a merchandise of prime numbers as follows:
60 = 5 × 3 × 2 × 2
As stool be seen from the example above, there are no composite numbers in the factorisation.
What is prime factoring?
Prime factorization is the decomposition of a composite number into a production of prime numbers. There are many another factoring algorithms, some more complicated than others.
Trial division:
One method for finding the heyday factors of a composite number is test sectionalization. Trial division is cardinal of the more fundamental algorithms, though it is highly tedious. It involves testing each whole number away dividing the composite number in question by the whole number, and determining if, and how many multiplication, the integer can divide the number evenly. As a simple example, below is the prime factorization of 820 using run division:
820 ÷ 2 = 410
410 ÷ 2 = 205
Since 205 is no longer divisible by 2, test the next integers. 205 cannot be equally divided by 3. 4 is not a prime number. It can however be divided aside 5:
205 ÷ 5 = 41
Since 41 is a prime number, this concludes the trial segmentation. Thus:
820 = 41 × 5 × 2 × 2
The products rear besides be written as:
820 = 41 × 5 × 22
This is in essence the "brute force" method for determining the bloom factors of a number, and though 820 is a simple example, information technology can get far more long-winded very speedily.
Prime decay:
Another common way to conduct flower factorization is referred to as flus decomposition, and can involve the utilization of a factor tree. Creating a factor tree involves breaking up the composite number into factors of the composite number, until all of the numbers racket are prime. In the example below, the prime factors are found by dividing 820 away a prime factor, 2, then continuing to divide the result until all factors are prime. The instance below demonstrates two slipway that a factor tree can be created using the number 820:
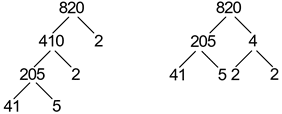
Thus, it can follow seen that the prime factorization of 820, in either case, again is:
820 = 41 × 5 × 2 × 2
While these methods work for small numbers (and there are many other algorithms), there is no known algorithmic rule for much large numbers, and it fire take a long period of fourth dimension for straight-grained machines to compute the prime factorizations of larger numbers; in 2009, scientists concluded a project using hundreds of machines to factor in the 232-digit number, RSA-768, and it took two geezerhood.
Prime factorization of frequent numbers
The following are the prime factorizations of some common numbers.
Meridian factorization of 2: superior number
Prime factorisation of 3: prime number
Prime factorization of 4: 22
Prime factorization of 5: prime number
Prime factorization of 6: 2 × 3
Prime factorization of 7: prime number
Prime factorization of 8: 23
Prime factorization of 9: 32
Prime factorization of 10: 2 × 5
Prime factorisation of 11: prime number
Prime factoring of 12: 22 × 3
Prime factorization of 13: prime phone number
Prime factorization of 14: 2 × 7
Blossom factoring of 15: 3 × 5
Meridian factorization of 16: 24
Prime factorization of 17: prime number
Prime factorisation of 18: 2 × 32
Prime factorization of 19: prime bi
Prime factorisation of 20: 22 × 5
Select factorization of 21: 3 × 7
Prime factorization of 22: 2 × 11
Ground factorization of 23: prime identification number
Prime factorization of 24: 23 × 3
Prime factorization of 25: 52
Prime factorization of 26: 2 × 13
Prime factorization of 27: 33
Prime factorization of 28: 22 × 7
Prime factorization of 29: prime number
Prime factorization of 30: 2 × 3 × 5
Prime factorization of 31: prime number
Prime factorization of 32: 25
Prime factorization of 33: 3 × 11
Prime factorization of 34: 2 × 17
Prime factorization of 35: 5 × 7
Prime factorisation of 36: 22 × 32
Prime factorisation of 37: prime number
Prize factorization of 38: 2 × 19
Prime factorization of 39: 3 × 13
Prime factorization of 40: 23 × 5
Heyday factorization of 41: prime number
Prime factoring of 42: 2 × 3 × 7
Prime factorization of 43: prime number
Prime quantity factorization of 44: 22 × 11
Prime factorization of 45: 32 × 5
Prime factorisation of 46: 2 × 23
Prime factorization of 47: prime list
Meridian factorization of 48: 24 × 3
Prime factoring of 49: 72
Prime factorization of 50: 2 × 52
Ground factorization of 51: 3 × 17
Prime factorization of 52: 22 × 13
Prime factorization of 53: efflorescence number
Prime factorisation of 54: 2 × 33
Prime factorisation of 55: 5 × 11
Prime factoring of 56: 23 × 7
Superior factorization of 57: 3 × 19
Prime factoring of 58: 2 × 29
Prime factorization of 59: prime number
Prime factorization of 60: 22 × 3 × 5
Prime factorisation of 61: prime number
Prime factorisation of 62: 2 × 31
Mature factorization of 63: 32 × 7
Prime factoring of 64: 26
Mature factorization of 65: 5 × 13
Prime factorization of 66: 2 × 3 × 11
Prime factorization of 67: prime number
Prime factorization of 68: 22 × 17
Prime factorization of 69: 3 × 23
Prime factorization of 70: 2 × 5 × 7
Quality factorization of 71: prize number
Prime factorisation of 72: 23 × 32
Prime factorization of 73: prime keep down
Prime factorization of 74: 2 × 37
Prime factorisation of 75: 3 × 52
Prime factorisation of 76: 22 × 19
Prime factoring of 77: 7 × 11
Prime factorization of 78: 2 × 3 × 13
Prime factorization of 79: prime number
Prime factorization of 80: 24 × 5
Prime factorization of 81: 34
Prime factorization of 82: 2 × 41
Prime quantity factorisation of 83: prime number
Quality factorization of 84: 22 × 3 × 7
Prime factorization of 85: 5 × 17
Prime factorization of 86: 2 × 43
Flus factorisation of 87: 3 × 29
Prime factorisation of 88: 23 × 11
Flus factorization of 89: prime number
Prime factorization of 90: 2 × 32 × 5
Prize factoring of 91: 7 × 13
Prime factorization of 92: 22 × 23
Prime factorization of 93: 3 × 31
Choice factorization of 94: 2 × 47
Prime factorisation of 95: 5 × 19
First factoring of 96: 25 × 3
Prime factorisation of 97: prime number
Prime factorization of 98: 2 × 72
Prime factorization of 99: 32 × 11
Prime factorization of 100: 22 × 52
Prime factorization of 101: prime number
Prime factorization of 102: 2 × 3 × 17
Prime factorization of 103: quality number
Prime factorization of 104: 23 × 13
Ground factoring of 105: 3 × 5 × 7
Prize factorization of 106: 2 × 53
Quality factorization of 107: prime number
Prime factoring of 108: 22 × 33
Prime factorization of 109: prime number
Prime factorization of 110: 2 × 5 × 11
Prime factorization of 111: 3 × 37
Select factorization of 112: 24 × 7
Prime factorisation of 113: superior number
Mature factorization of 114: 2 × 3 × 19
Prime factoring of 115: 5 × 23
Prime factorization of 116: 22 × 29
Prime of life factorization of 117: 32 × 13
Peak factorization of 118: 2 × 59
Select factorization of 119: 7 × 17
Prime factorization of 120: 23 × 3 × 5
Prime factorization of 121: 112
Bloom factorization of 122: 2 × 61
Prime factorisation of 123: 3 × 41
Prime factorization of 124: 22 × 31
Prime factorization of 125: 53
Prime factorization of 126: 2 × 32 × 7
Prime factorization of 127: prime phone number
Prime factoring of 128: 27
Prime factorization of 129: 3 × 43
Prime factorization of 130: 2 × 5 × 13
Prime factorisation of 131: prime number
Prime factoring of 132: 22 × 3 × 11
Prime factorization of 133: 7 × 19
Prime factorization of 134: 2 × 67
Superior factorization of 135: 33 × 5
Prime factorization of 136: 23 × 17
Prime factoring of 137: meridian number
Prime factorization of 138: 2 × 3 × 23
Prime factorization of 139: select number
Prime factorization of 140: 22 × 5 × 7
Undercoat factorization of 141: 3 × 47
Prime factorisation of 142: 2 × 71
Prime factoring of 143: 11 × 13
Premier factorization of 144: 24 × 32
Prime factorization of 145: 5 × 29
Prime factoring of 146: 2 × 73
Meridian factorization of 147: 3 × 72
Blossom factorization of 148: 22 × 37
Prime factorization of 149: bloom list
Prime factorisation of 150: 2 × 3 × 52
Prime factorisation of 200: 23 × 52
Meridian factorization of 300: 22 × 3 × 52
Prime factoring of 400: 24 × 52
Prime factorization of 500: 22 × 53
Prime factorization of 600: 23 × 3 × 52
Prime factoring of 700: 22 × 52 × 7
Prime factoring of 800: 25 × 52
Prime factorization of 900: 22 × 32 × 52
Ground factorization of 1000: 23 × 53
what is the prime factorization of 525 using exponents
Source: https://www.calculator.net/prime-factorization-calculator.html
Posting Komentar untuk "what is the prime factorization of 525 using exponents"